Chapter 1, Automata: The Methods and the Madness

This series of documents in this column are summarized from this book: Introduction to automata theory, languages, and computation.[1]

Why Study Automata Theory?

Introduction to Finite Automata

Automata theory is the study of abstract computing devices or "machines".

Finite automata are a useful model for many important kinds of hardware and software.

• Software for designing and checking the behavior of digital circuits.
• The "lexical analyzer" of a typical compiler, that is, the compiler component that breaks the input text into logical units, such as identifiers, keywords, and punctuation.
• Software for scanning large bodies of text, such as collections of Web pages, to find occurrences of words, phrases,or other patterns.
• Software for verifying systems of all types that have a finite number of distinct states, such as communications protocols or protocols for secure exchange of information.

Perhaps the simplest nontrivial finite automaton is an on/off switch (Figure 1).

Figure 1. A simple finite automaton.

Figure 2 shows another finite automaton that could be part of a lexical analyzer. The job of this automaton is to recognize the keyword then. It thus needs five states, each of which represents a different position in the word then that has been reached so far. These positions correspond to the prefixes of the word, ranging from the empty string (i.e., nothing of the word has been seen so far) to the complete word. We could consider the state "then" as accepting state.

Figure 2. A finite automaton modeling recognition of then.

Structural Representations

There are two important notations that are not automaton-like, but play an important role in the study of automata and their applications.

• Grammars are useful models when designing software that processes data with a recursive structure. The best-known example is a "parser", the component of a compiler that deals with the recursively nested features of the typical programming language, such as expressions-arithmetic, conditional, and so on. For instance,a grammatical rule like $E\Rightarrow E+E$ states that an expression can be formed by taking any two expressions and connecting them by a plus sign; this rule is typical of how expressions of real programming languages are formed. Later, we'll introduce context-free grammars, as they are usually called.
• Regular Expressions also denote the structure of data, especially text strings. The patterns of strings they describe are exactly the same as what can be described by finite automata. The style of these expressions differs significantly from that of grammars, and we shall content ourselves with a simple example here. The UNIX-style regular expression [A-Z][a-z]*[ ][A-Z][A-Z], represents capitalized words followed by a space and two capital letters. This expression represents patterns in text that could be a city and state, e.g., Ithaca NY. It misses multiword city names, such as Palo Alto CA, which could be captured by the more complex expression [A-Z][a-z]*([ ][A-Z] [a-z]*)*[ ][A-Z][A-Z].

Automata and Complexity

Automata are essential for the study of the limits of computation. As we mentioned in the introduction to the chapter, there are two important issues:

• What can a computer do at all? This study is called "decidability," and the problems that can be solved by computer are called "decidable."
• What can a computer do efficiently? This study is called "intractability," and the problems that can be solved by a computer using no more time than some slowly growing function of the size of the input are called "tractable." Often,we take all polynomial functions to be "slowly growing," while functions that grow faster than any polynomial are deemed to grow too fast.

Introduction to Formal Proof

Perhaps more than other core subjects of computer science, automata theory lends itself to natural and interesting proofs, both of the deductive kind (a sequence of justified steps) and the inductive kind (recursive proofs of a parameterized statement that use the statement itself with "lower" values of the parameter).

Deductive Proofs

A deductive proof consists of a sequence of statements whose truth leads us from some initial statement, called the hypothesis or the given statement(s), to a conclusion statement. Each step in the proof must follow, by some accepted logical principle, from either the given facts, or some of the previous statements in the deductive proof, or a combination of these.

The hypothesis may be true or false, typically depending on values of its parameters. Often, the hypothesis consists of several independent statements connected bya logical AND. In those cases, we talk of each of these statements as a hypothesis, or as a given statement.

The theorem that is proved when we go from a hypothesis $H$ to a conclusion $C$ is the statement "if $H$ then $C$." We say that $C$ is deduced from $H$.

Reduction to Definitions

In many other theorems, including many from automata theory, the terms used in the statement may have implications that are less obvious.

tip

If you are not sure how to start a proof, convert all terms in the hypothesis to their definitions.

Here is an example of a theorem that is simple to prove once we have expressed its statement in elementary terms. It uses the following two definitions:

• A set $S$ is finite if there exists an integer $n$ such that $S$ has exactly $n$ elements in a set $S$. We write $\| S\|=n$, where $\|S\|$ is used to denote the number of elements in a set $S$. If the set $S$ is not finite, we say $S$ is infinite. Intuitively, an infinite set is a set that contains more than any integer number of elements.
• If $S$ and $T$ are both subsets of some set $U$, then $T$ is the complement of $S$ (with respect to $U$) if $S\cup T=U$ and $S\cap T=\emptyset$. That is, each element of $U$ is in exactly those elements off $U$ that are not in $S$.

Theorem

Let $S$ be a finite subset of some infinite set $U$. Let $T$ be the complement of $S$ with respect to $U$. Then $T$ is infinite.

Other Theorem Forms

Ways of Saying "If-Then"

Here are some of the other ways in which "if $H$ then $C$" might appear.

• $H$ implies $C$.
• $H$ only if $C$.
• $C$ if $H$.
• Whenever $H$ holds, $C$ follows.
  • If $H$ holds, then $C$ follows.
  • Whenever $H$ holds, $C$ holds.

In formal logic one often sees the operator $\rightarrow$ in place of "if-then". That is, the statement "if $H$ then $C$" could appear as $H\rightarrow C$ in some mathematical literature.

If-And-Only-If Statements

In formal logic, one may see the operator $\Leftrightarrow$ or $\equiv$ to denote an "if-and-only-if" statement. That is, $A\equiv B$ and $A\Leftrightarrow B$ mean the same as "$A$ if and only if $B$".

tip

When proving an if-and-only-if statement, it is important to remember that you must prove both the "if" and "only-if" parts. Sometimes, you will find it helpful to break an if-and-only-if into a succession of several equivalences. That is, to prove "$A$ if and only if $B$", you might first prove "$A$ if and only if $C$" and then prove "$C$ if and only if $B$".

Theorem

Let $x$ be a real number. Then $\lfloor x\rfloor=\lceil x\rceil$ if and only if $x$ is an integer.

---

$\lfloor x\rfloor$, the floor of a real number, is the greatest integer equal to or less than $x$.

$\lceil x\rceil$, the ceil of a real number, is the least integer equal to or greater than $x$.

Theorems That Appear Not to Be If-Then Statements

Sometimes,we encounter a theorem that appears not to have a hypothesis. An example is the well-known fact from trigonometry:

Pythagorean Identity

Theorem

$\sin^2\theta+\cos^2\theta=1$

Additional Forms of Proof

In this section,we take up several additional topics concerning how to construct proofs:

• Proofs about sets.
• Proofs by contradiction.
• Proofs by counterexample.

Proving Equivalences About Sets

The Distributive Law of Union Over Intersection

Theorem

$R\cup(S\cap T)=(R\cup S)\cap(R\cup T)$

---

An element $x$ is in $R\cup(S\cap T)$ if and only if $x$ is in $(R\cup S)\cap(R\cup T)$.

The elements of $R\cup(S\cap T)$ are all and only the elements of $(R\cup S)\cap(R\cup T)$.

The Contrapositive

Every if-then statement has an equivalent form that in some circumstances is easier to prove. The contrapositive of the statement "if $H$ then $C$" is "if not $C$ then not $H$".

A statement and its contrapositive are either both true or both false,so we can prove either to prove the other.

Proof by Contradiction

Another way to prove a statement of the form "if $H$ then $C$" is to prove the statement: $H$ and not $C$ implies falsehood.

Counterexamples

In real life,we are not told to prove a theorem. Rather,we are faced with something that seems true - a strategy for implementing a program for example - and we need to decide whether or not the "theorem" is true. To resolve the question, we may alternately try to prove the theorem, and if we cannot, try to prove that its statement is false.

Theorems generallyare statements about an infinite number of cases, perhaps all values of its parameters. Indeed, strict mathematical convention will only dignify a statement with the title "theorem" if it has an infinite number of cases; statements that have no parameters, or that apply to only a finite number of values of its parameter(s)are called observations. It is sufficient to show that an alleged theorem is false in any one case in order to show it is not a theorem. The situation is analogous to programs, since a program is generally considered to have a bug if it fails to operate correctly for even one input on which it was expected to work.

It often is easier to prove that a statement is not a theorem than to prove it is a theorem.

Inductive Proofs

There is a special form of proof, called "inductive", that is essential when dealing with recursively defined objects.

Inductions on Integers

Suppose we are given a statement $S(n)$, about an integer $n$, to prove. One common approach is to prove 2 things:

• The basis, where we show $S(i)$ for a particular integer $i$. Usually, $i=0$ or $i=1$, but there are examples where we want to start at some higher $i$, perhaps because the statement $S$ is false for a few small integers.
• The inductive step, where we assume $n\geq i$, where $i$ is the basis integer, and we show that "if $S(n)$ then $S(n+1)$".

The Induction Principle: If we prove $S(i)$ and we prove that for all $n\geq i$,$S(n)$ implies $S(n+1)$, then we may conclude $S(n)$ for all $n\geq i$.

More General Forms of Integer Inductions

Sometimes an inductive proof is made possible only by usinga more general scheme than the one proposed here, where we proved a statement $S$ for one basis value and then proved that "if $S(n)$ then $S(n+1)$". Two important generalizations of this scheme are:

• We can use several basis cases. That is, we prove $S(i),S(i+1),\dots,S(j)$ for some $j>i$.

• In proving $S(n+1)$, we can use the truth of all the statements

  $S(i),S(i+1),\dots,S(j)$

  rather than just using $S(n)$. Moreover, if we have proved basis cases up to $S(j)$, then we can assume $n\geq j$, rather than just $n\geq i$.

Structural Inductions

Like inductions, all recursive definitions have a basis case, where one or more elementary structures are defined, and an inductive step, where more complex structures are defined in terms of previously defined structures.

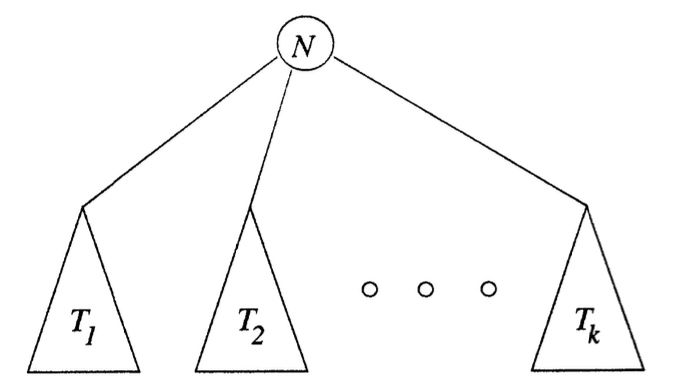
Inductive construction of a tree

Definition

Basis: A single node is a tree, and that node is the root of the tree.

Induction: If $T_1,T_2,\dots,T_k$ are trees, then we can form a new tree as follows:

• Begin with a new node $N$, which is the root of the tree.
• Add copies of all the trees $T_1,T_2,\dots,T_k$.
• Add edges from node $N$ to the roots of each of the trees $T_1,T_2,\dots,T_k$.

Figure 3 shows the inductive construction of a tree with the root $N$ from $k$ smaller trees.

Figure 3. Inductive construction of a tree.

Mutual Inductions

Sometimes, we cannot prove a single statement by induction, but rather need to prove a group of statements $S_1(n),S_2(n),\dots,S_k(n)$ together by induction on $n$.

Strictly speaking, proving a group of statements is no different from proving the conjunction (logical AND) of all the statements.

However, when there are really several independent statements to prove, it is generally less confusing to keep the statements separate and to prove them all in their own parts of the basis and inductive steps. We call this sort of proof mutual induction.

We can abstract the pattern for all mutual inductions:

• Each of the statements must be proved separately in the basis and in the inductive step.
• If the statements are "if-and-only-if," then both directions of each statement must be proved, both in the basis and in the induction.

The Central Concepts of Automata Theory

Alphabets

Alphabets

Definition

An alphabet is a finite, nonempty set of symbols. Conventionally, we use the symbol $\Sigma$ for an alphabet. Common alphabets include:

• $\Sigma=\{0,1\}$, the binary alphabet.
• $\Sigma=\{a,b,\dots,z\}$, the set of lower-case letters.
• The set of all ASCII characters, or the set of all printable ASCII characters.

Strings

Strings

Definition

A string (or sometimes word) is a finite sequence od symbols chosen from some alphabet.

The Empty String

The empty string is the string with zero occurrences of symbols. This string, denoted $\epsilon$, is a string that may be chosen from any alphabet whatsoever.

Length of a String

It is often useful to classify strings by their length, that is, the number of positions for symbols in the string. For instance, 01101 has length 5.

The standard notation for the length of a string $w$ is $|w|$. For example, $|1011|=4$.

Power of an Alphabet

If $\Sigma$ is an alphabet, we can express the set of all strings of a certain length from that alphabet by using an exponential notation. We define $\Sigma^k$ to be the set of strings of length $k$, each of whose symbols is in $\Sigma$.

Note that $\Sigma^0=\{\epsilon\}$, regardless of what alphabet $\Sigma$ is.

The set of all strings over an alphabet $\Sigma$ is $\Sigma^{*}$, i.e. $\{0,1\}=\{\epsilon,0,1,00,01,10,11,000,\dots\}$. That is, $\Sigma^{*}=\Sigma^0\cup\Sigma^1\cup\Sigma^2\cup\dots$.

The set of nonempty strings from alphabet $\Sigma$ is denoted $\Sigma^+$. Thus, two appropriate equivalences are:

• $\Sigma^+=\Sigma^1\cup\Sigma^2\Sigma^3\cup\dots$;
• $\Sigma^*=\Sigma^+\cup\{\epsilon\}$.

tip

$\Sigma$ is an alphabet, $\Sigma^1$ is a set of strings (length = 1).

Concatenation of Strings

Let $x$ and $y$ be strings, then $xy$ denotes the concatenation of $x$ and $y$. That is, the string formed by making a copy of $x$ and following it by a copy of $y$. More precisely, if $x$ is the string composed of $i$ symbols $x=a_1a_2\cdots a_i$ and $y$ is the string composed of $j$ symbols $y=b_1b_2\cdots b_j$, then $xy$ is the string of length $i+j:\;xy=a_1a_2\cdots a_ib_1b_2\cdots b_j$.

Languages

A set of strings all of which are chosen from some $\Sigma^*$, where $\Sigma$ is a particular alphabet, is called a language. If $\Sigma$ is an alphabet, and $L\subseteq \Sigma^*$, then $L$ is a language over $\Sigma$.

Notice that a language over $\Sigma$ need not include strings with all the symbols of $\Sigma$, so once we have established that $L$ is a language over $\Sigma$, we also know it is a language over any alphabet that is a superset of $\Sigma$.

$\emptyset$, the empty language, is a language over any alphabet.

$\{\epsilon\}$, the language consisting of only the empty string, is also a language over any alphabet.

$\emptyset \neq \{\epsilon\}$, the former has no strings and the latter has one string.

The only important constraint on what can be a language is that all alphabets are finite. Thus languages, although they can have. an infinite number of strings, are restricted to consist of strings drawn from one fixed, finite alphabet.

It is common to describe a language using a "set-former":

$$\{w|somthing\;about\;w\}.$$

For example:

$$\{w|w\;is\;a\;binary\;integer\;that\;is\;prime\}.$$

It is also common to replace $w$ by some expression with parameters and describe the strings in the language by stating conditions on the parameters. For example:

$$\{0^n1^n|n\geq 1\}.$$

which is $\{01,0011,000111,\dots\}$.

Problems

In automata theory, a problem is the question of deciding whether a given string is a member of some particular language. It turns out, as we shall see, that anything we more colloquially call a "problem" can be expressed as membership in a language. More precisely, if $\Sigma$ is an alphabet, and $L$ is a language over $\Sigma$, then the problem $L$ is:

• Given a string $w$ in $\Sigma^*$, decide whether or not $w$ is in $L$.

Reference

1. J. E. Hopcroft, R. Motwani, and J. D. Ullman, Introduction to automata theory, languages, and computation, 2nd edition, vol. 32, no. 1. New York, NY, USA: ACM Press, 2001, pp. 60-65.