Chapter 2, Finite Automata

Deterministic Finite Automaton, DFA

A deterministic finite automaton consists of:

• A finite set of states, often denoted $Q$.
• A finite set of input symbols, often denoted $\Sigma$.
• A transition function that takes as arguments a state and an input symbol and returns a state, often denoted $\delta$. In our formal graph representation of automata, $\delta$ was represented by arcs between states and the labels on the arcs. If $q$ is a state, and $a$ is an input symbol, then $\delta(q,a)$ is that state $p$ such that there is an arc labeled $a$ from $q$ to $p$.
• A start state, one of the states in $Q$.
• A set of final or accepting states $F$. The set $F$ is a subset of $Q$.

A deterministic finite automaton can often be referred to by its acronym: DFA. The most succinct representation of a DFA is a listing of the five components above. In proofs we often talk about a DFA in "five-tuple" notation:

$$A=(Q,\Sigma,\delta,q_0,F)$$

where $A$ is the name of DFA, $Q$ is its set of states, $\Sigma$ its input symbols, $]delta$ its transition function, $q_0$ its start state, and $F$ its set of accepting states.

How a DFA Processes Strings

The first thing we need to understand about a DFA is how the DFA decides whether or not to "accept" a sequence of input symbols. The "language" of the DFA is the set of all strings that the DFA accepts. Suppose $a_1a_2\cdots a_n$ is a sequence of input symbols. We start out with the DFA in its start state, $q_0$. We consult the transition function $\delta$, say $\delta(q_0,a_1)=q_1$ to find the state that the DFA $A$ enters after processing the first input symbol $a_1$. We process the next input symbol, $a_2$, by evaluating $\delta(q_1,a_2)$; let us suppose this state is $q_2$. We continue in this manner, finding states $q_3,q_4,\dots,q_n$ such that $\delta(q_{i-1},a_i)=q_i$ for each $i$. If $q_n$ is a member of $F$, then the input $a_1a_2\cdots a_n$ is accepted, and if not then it is "rejected".

Simpler Notations for DFA's

Specifying a DFA as a five-tuple with a detailed description of the ð transition function is both tedious and hard to read. There are two preferred notations for describing automata:

• A transition diagram, which is a graph such as the ones we saw before.
• A transition table, which is a tabular listing of $\delta$ function, which by implication tells us the set of states and the input alphabet.

Transition Diagrams

A transition diagram for a DFA $A=(Q,\Sigma,\delta,q_0,F)$ is a graph defined as follows:

• For each state in $Q$ there is a node.
• For each state $q$ in $Q$ and each input symbol $a$ in $\Sigma$, let $\delta(q,a)=p$.Then the transition diagram has an arc from node $q$ to node $p$, labeled $a$. If there are several input symbols that cause transitions from $a$ to $p$, then the transition diagram can have one arc, labeled by the list of these symbols.
• There is an arrow into the start state $q_0$, labeled Start. This arrow does not originate at any node.
• Nodes corresponding to accepting states (those in $F$) are marked by a double circle. States noe in $F$ have a single circle.

Figure 1 shows the transition diagram for the DFA that we designed before.

Figure 1. The transition diagram for the DFA accepting all strings with a substring "01".

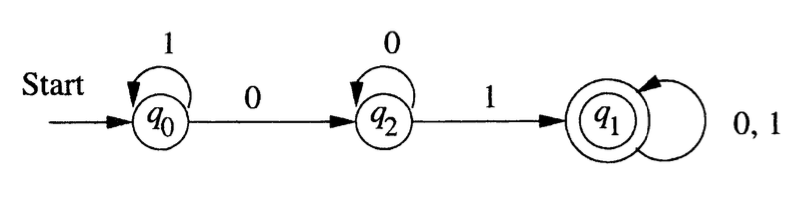
Transition Tables

A transition table is a conventional, tabular representation of a function like $\delta$ that takes two arguments and returns a value. The rows of the table correspond to the states, and the columns correspond to the inputs. The entry for the row corresponding to state $q$ and the column corresponding to input $a$ is the state $\delta(q,a)$.

Figure 2 is a transition diagram.

Figure 2. Transition table for the DFA (corresponding to Figure 1).

Nondeterministic Finite Automata, NfA

A "nondeterministic" finite automaton (NFA) has the power to be in several states at once. This ability is often expressed as an ability to "guess" something about its input. The NFA's accept exactly the regular languages, just as DfA's do. They are often more succinct and easier to design than DFA's, and we can always convert an NFA to a DFA. The latter may have exponentially more states than the NFA; fortunately, cases of this type are rare.

An Informal View of Nondeterministic Finite Automata

Figure 3 shows a nondeterministic finite automaton, whose job is to accept all and only the strings of 0's and 1's that end in "01".

Figure 3. An NFA accepting all strings that end in "01".

Definition of Nondeterministic Finite Automata

An NFA is represented essentially like a DFA:

$$A=(Q,\Epsilon,\delta,q_0,F)$$

where:

• $Q$ is a finite set of states.
• $\Epsilon$ is a finite set of input symbols.
• $q_0$, a member of $Q$, is the start state.
• $F$, a subset of $Q$, is the set of final (or accepting) states.
• $\delta$, the transition function is a function that takes a state in $Q$ and an input symbol in $\Epsilon$ as arguments and returns a subset of $Q$. Notice that the only difference between an NFA and a DFA is in the type of value that $\delta$ returns: a set of states in the case of an NFA and a single state in the case of a DFA.